Essay on: "Testing of the Seismic Gap Hypothesis in a Model with Realistic Earthquake Statistics"
- Essay analysis by: G. Petrillo1 and J. Zhuang1
- Article authors: G. Petrillo1,2, A. Rosso3, and E. Lippiello2
- 1The Institute of Statistical Mathematics, Research Organization of Information and Systems, Tokyo, Japan,
- 2Department of Mathematics and Physics, University of Campania “L. Vanvitelli”, Caserta, Italy,
- 3LPTMS, CNRS, University Paris-Sud, Université Paris-Saclay, Orsay, France
- Eugenio Lippiello, Giuseppe Petrillo, François Landes, Alberto Rosso (2019). Fault Heterogeneity and the Connection between Aftershocks and Afterslip. Bulletin of the Seismological Society of America, 109 (3): 1156-1163. doi: https://doi.org/10.1785/0120180244.
- Petrillo, G., Lippiello, E., Landes, F.P. et al. (2020). The influence of the brittle-ductile transition zone on aftershock and foreshock occurrence. Nat Commun 11, 3010. https://doi.org/10.1038/s41467-020-16811-7.
- Petrillo, G., Rosso, A., & Lippiello, E. (2022). Testing of the seismic gap hypothesis in a model with realistic earthquake statistics. Journal of Geophysical Research: Solid Earth, 127, e2021JB023542. https://doi.org/10.1029/2021JB023542
- N. Wetzler, T. Lay, E. E. Brodsky, H. Kanamori (2018). Systematic deficiency of aftershocks in areas of high coseismic slip for large subduction zone earthquakes. Sci. Adv. 4, eaao3225.
The earthquake occurrence is a singular characteristic of every part of the globe, but is characterized by statistical laws that are universal, regardless of the geographical location. The temporal and spatial correlations are a striking example.
In the paper “Testing of the Seismic Gap Hypothesis in a Model with Realistic Earthquake Statistics” the authors propose a new concept of spring block-like model coupling an elastic layer subject to a velocity weakening heterogeneous friction, to a second layer where friction is velocity strengthening (Fig.1). It is shown that by means of this extremely minimal model, with only two ingredients, most relevant earthquake statistical features, such as the Gutenberg-Richter law, the Omori law, the productivity law and the spatial clustering of aftershocks are recovered.
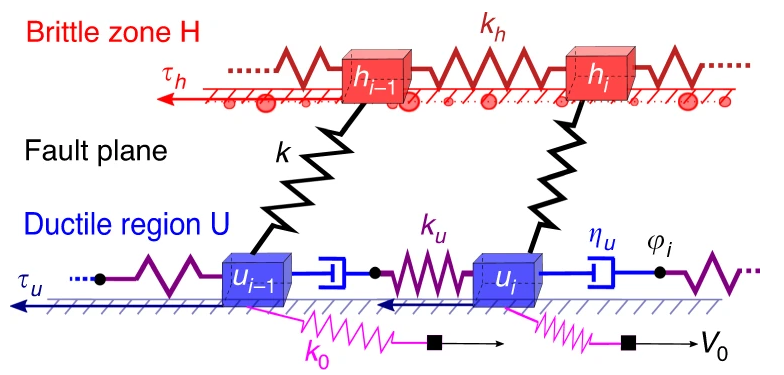
Fig.1. Mechanical sketch of the model (one-dimensional cut: the other direction is orthogonal to the plane). The fault plane H is subject to velocity-weakening friction τh, in the form of randomly placed pinning points (red disks) with different pinning strength (disk radius). The ductile region U is subject to velocity-strengthening friction τu, and is pulled at constant velocity V0 by distant regions. Within this ductile region, interactions are viscoelastic (Maxwell model), with dashpots having viscosity ηu and elasticity ku. The relative elongations of dashpots around site i is denoted zi = φi − ui − (φi−1 − ui−1). The two layers are connected elastically with a stiffnessk.
The extensive simulations that can be obtained with this model, allow to test the seismic gap hypothesis. Indeed, the estimate of the occurrence probability of the next big shock on the basis of the time delay from the last earthquake still represents a big challenge in the seismological community. The problem is that this issue cannot be addressed only on the basis of historical catalogs which contain too few well documented big shocks, and decades of future observations appear necessary.
Interestingly, this model confirms some of the recent results found in the literature concerning the relationship between the spatial organization of the aftershocks and the profile of the slipped area of the mainshock. By carrying out extensive tests it is possible to show that earthquakes do not repeat regularly in time, however it is possible to extract some probabilistic information on the time of occurrence of the next earthquake also and above all on the basis of the percentage of aftershocks that occur inside (or outside) of mainshock slip contour (Fig.2).
Summarizing this model shows that even if the next earthquake will probably occur on a gap region, its timing is quite irregular and weakly depends on the time delay of that region from the previous slip. Accordingly, the strict seismic cycle hypothesis where large earthquakes are roughly periodic in time would have to be discarded. Interestingly, our study demonstrates the usefulness of the information contained in the spatial organization of aftershocks which can be used to have insights on the timing of the next large earthquake, coherently with the direction identified by Wetzler et al. (2018) from real seismic data. Moreover the conjecture proposed by Wetzler et al (2018) that the temporal distance to the subsequent large earthquake is smaller the larger is the percentage of aftershocks inside the high slip contour of the mainshock is demonstrated (Fig.2).
We support the importance of this result because, although it is difficult to obtain the value of the stress present on the fault and then possibly estimate the recurrence time, the number of aftershocks is an easily accessible quantity, therefore any seismic forecasts on the time of occurrence can be carried out.
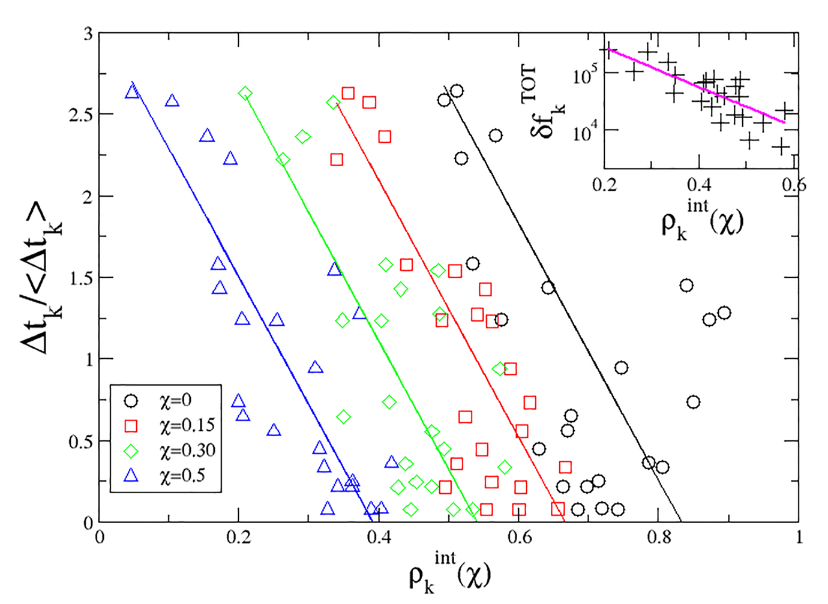
Fig.2. The parametric plot of the recurrence time versus the percentage of the aftershocks occurred inside the mainshock slip contour. Different colors correspond to different values of χ, which is a value that indicate different definition of mainshock slip contour. Colored continuous lines represent the best linear fit of the data. (Inset) The parametric plot of the total stress drop versus the percentage of the aftershocks occurred inside the mainshock slip contour for χ = 0.3. The magenta line is the best least squares fit.